Quand on prononce le mot « fractal » vient immédiatement à l’esprit le nom de Benoit Mandelbrot qui a découvert l’ensemble qui porte son nom. Mais comme toujours en sciences, beaucoup d’autres chercheurs et découvreurs avaient en quelque sorte déblayé le terrain…

Tout d’abord les mathématiciens qui ont créé les outils, les concepts et l’algèbre pour manipuler les nombres complexes dits « imaginaires » qui interviennent dans les équations fractales. Le premier (car il y a toujours un précurseur) fut Girolamo Cardano (Cardan) qui fut dès l’an 1545 le premier mathématicien à imaginer l’existence de racines carrées de nombres négatifs. Quand on y pense, il fallait déjà avoir l’esprit bien perché pour s’emmerder à cette époque avec de tels concepts ! Imaginez : racine carrée de 2, facile : 1.41421356237… etc (nombre irrationnel). Mais racine carrée de -2 ? Quel nombre multiplié par lui même donne-t-il « moins deux » ? Vous avez 1 heure… D’ou l’introduction des fameux nombres imaginaires…

Ensuite vint Bombelli, suivi au cours du temps par les plus grands théoriciens des mathématiques comme Leibnitz, Descartes, Euler, Gauss, Cauchy, Boole, Riemann, Hamilton…

Ensuite les « fractalistes » et autres explorateurs du « chaos » : Fatou, Julia, Lorenz et un certain Feigenbaum dont la tête de savant fou n’est pas sans évoquer le film « Retour vers le futur » comme on peut le voir en couverture de cet article, illustration réalisée à partir d’un portrait original de Gunilla Feigenbaum.

Plongée dans le chaos

Mitchell Jay Feigenbaum docteur au MIT, puis au Laboratoire de Los Alamos a découvert en 1975, en étudiant les « suites logistiques », un scénario de transition vers le chaos par doublement de période. De quoi s’agit-il ?

Les suites logistiques caractérisent de nombreux phénomènes de « croissance sous contrainte », comme une population de bactéries avec un quota de nourriture donné, par exemple. La population croit, consomme la nourriture, puis décroit. De même, la population de fleurs dans un parterre, ou les courants de convection d’un liquide : en fait des quantités de phénomènes physiques et qu’on rencontre en particulier dans la nature. On peut les modéliser avec des équations récursives qui sont de la forme :

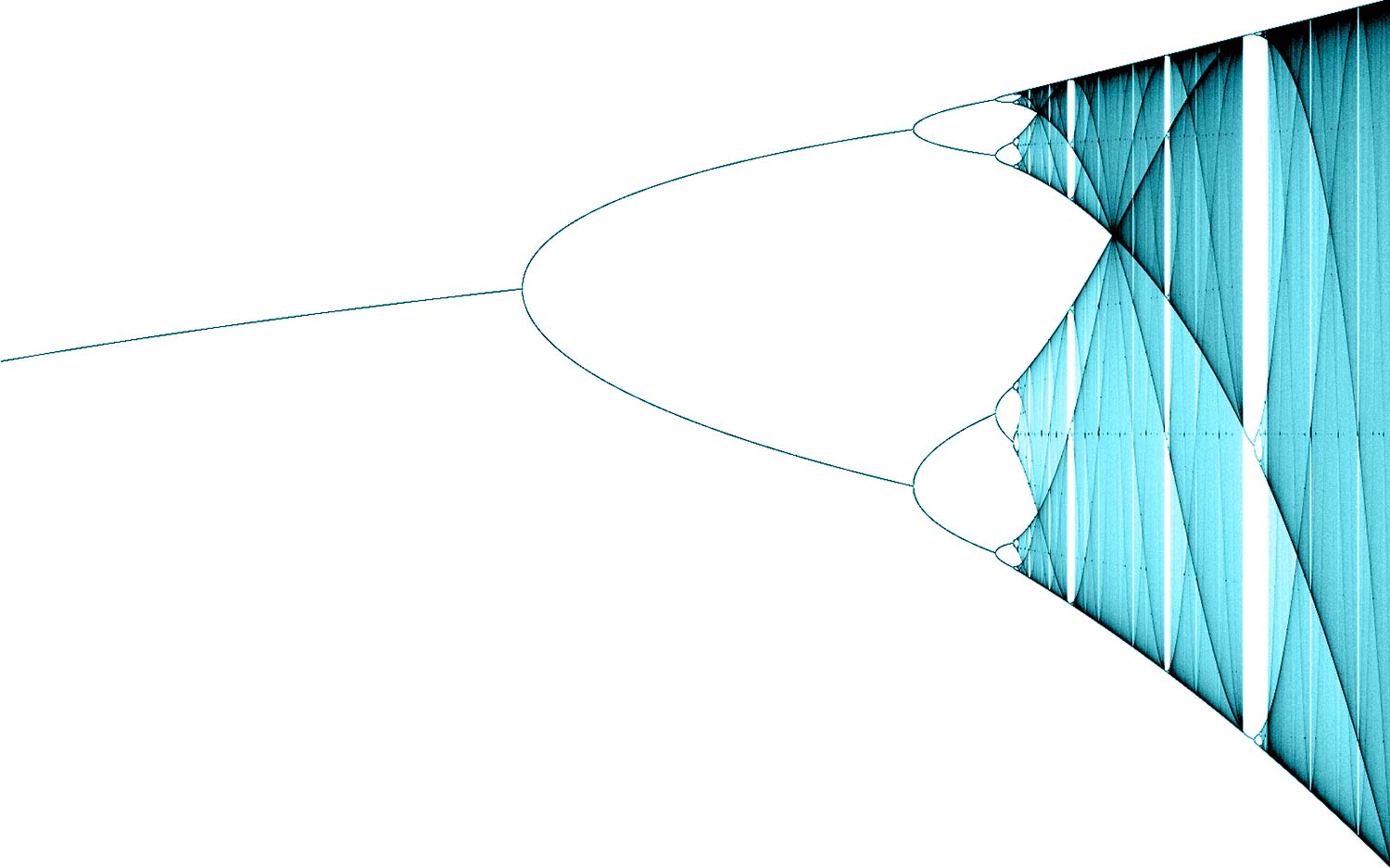
On peut faire varier le coefficient « r » en fonction des phénomènes étudiés. En construisant un graphe avec les différentes valeurs de « n » (En fait en multipliant les « itérations »), on arrive à des diagrammes caractéristiques baptisés « diagrammes de bifurcation ». On assiste à une division en deux puis en quatre, puis, assez rapidement des divisions erratiques, imprévisibles, relevant du chaos. Ces zones ressemblent à une « poussière de Cantor » mais entrecoupées de zones « blanches » ou les divisons sont déterminées et non plus chaotiques

Quand on fait osciller un pendule double par exemple, il est facile de prévoir la position qu’il va occuper dans l’espace. Tout au moins lors des premières oscillations. Car très vite, le mouvement devient « chaotique » et incroyablement sensible aux « conditions initiales » (le fameux « effet papillon »), autrement dit : la seule chose que l’on sache est qu’il est impossible justement de prévoir sa position ! Ainsi vont les vagues, les tempêtes solaires, les séismes et éruptions, la forme des nuages et même les courbes de propagation du virus COVID19. Le climat, enfin… Petit clin d’oeil amical aux devins capables de prévoir les fluctuations futures du climat terrestre alors que toute la science du Chaos nous explique le contraire… Les mathématiciens et physiciens doivent être tous des « climato-sceptiques ». Et en fait ils le sont ! En tout cas ceux que j’ai eu la chance d’interviewer ou de lire… Passons. Terrain miné.

Mais il y a encore plus fort… Feigenbaum a montré que, après un nombre suffisant d’itérations, les motifs se répètent quand on zoome (comme on peut le voir sur le diagramme ci-dessus) avec une échelle de forme toujours la même, ce qui rappelle fortement les fractales. Et pour cause : ces diagrammes sont eux aussi fractals ! Et il a observé que ces courbes déterminent une sorte de « valeur d’étirement », un facteur d’échelle de transformation des figures fractales. Une valeur qui lui est apparue constante, à toutes les échelles ! En effet, par le calcul il a montré qu’il s’agit là de deux constantes « universelles », comme peut l’être le nombre « Pi« , baptisées depuis nombres de Feigenbaum : 2,502908… et 4,66920166… Ce sont des nombres irrationnels (avec un nombre de décimales infinies) et sans doute transcendants, mais ce n’est pas démontré (les matheux sont pinailleurs)…

Ce qui est magique c’est qu’on retrouve ces constantes et la forme caractéristique de ces diagrammes dans toutes sortes de phénomènes aussi divers que les battements cardiaques, la dynamique des nuages, les courants de convection dans l’atmosphère, la dynamique de la houle marine, la répartition des cristaux dans une géode d’améthyste, le dessin des robes des poissons ou des papillons, tous les phénomènes de la turbulence et en fait, une majorité de phénomènes observables et qui constituent notre monde observable. Une vérité cachée au coeur du Chaos…

« Toi aussi, dessine ton diagramme de Feigenbaum ! »

Il est possible de générer des diagrammes de bifurcation de suites logistiques avec un certain nombre de logiciels scientifiques, notamment MathLab, ou Mathematica, avec pour ce dernier de larges sections dédiées à ces diagrammes, mais aussi avec un outil dédié, créé par un des gourous du Fractal Forum répondant au doux pseudo (encore un pseudo !) de Bkercso (on n’en saura pas plus).

Bifurcation Fractal Plotter pour Windaube peut ainsi calculer 19 types différents de systèmes chaotiques y compris les systèmes physiques doubles comme les pendules doubles et les balles rebondissantes sur deux toboggans. On peut utiliser jusqu’à 20 processeurs et générer des images avec une résolution sans limites. Si ce n’est les temps de rendus : l’auteur parle de dizaines de jours…

Mais pas de cerise et pas de gâteau : le logiciel « fonctionne » sans interface et il faut rentrer à la main des chemins de fichiers interminables ou copier/coller sous Windows un fichier de configuration en mode texte dans lequel on doit indiquer les différents paramètres (abscons, bien entendu, si on est pas un spécialiste des systèmes chaotiques).

Pour ce que j’en ai compris, le moindre réglage passe par des instructions à rentrer dans ce fichier ce qui dépasse mes compétences et aussi par l’emploi d’un autre logiciel Win : IrFanView (pour le zoom). Bref. Ma question est toujours la même : pourquoi s’entêter à programmer des saloperies pareilles sans faire l’effort (minimal) d’une interface un tantinet conviviale ? Mystère. Ces gens là aiment sans doute rester entre eux à coups de lignes de commandes…

Mais je suis de mauvaise foi, le package contient un « fichier d’aide » en .pdf. Bon courage. A droite, mon premier essai en bleu sur fond noir, rendu en 2 secondes m’indique le programme. Information dont je n’ai personnellement rien à faire alors que tant d’autres qui me seraient bien utiles sont manquantes ! Rhaaaaaa je les hais !

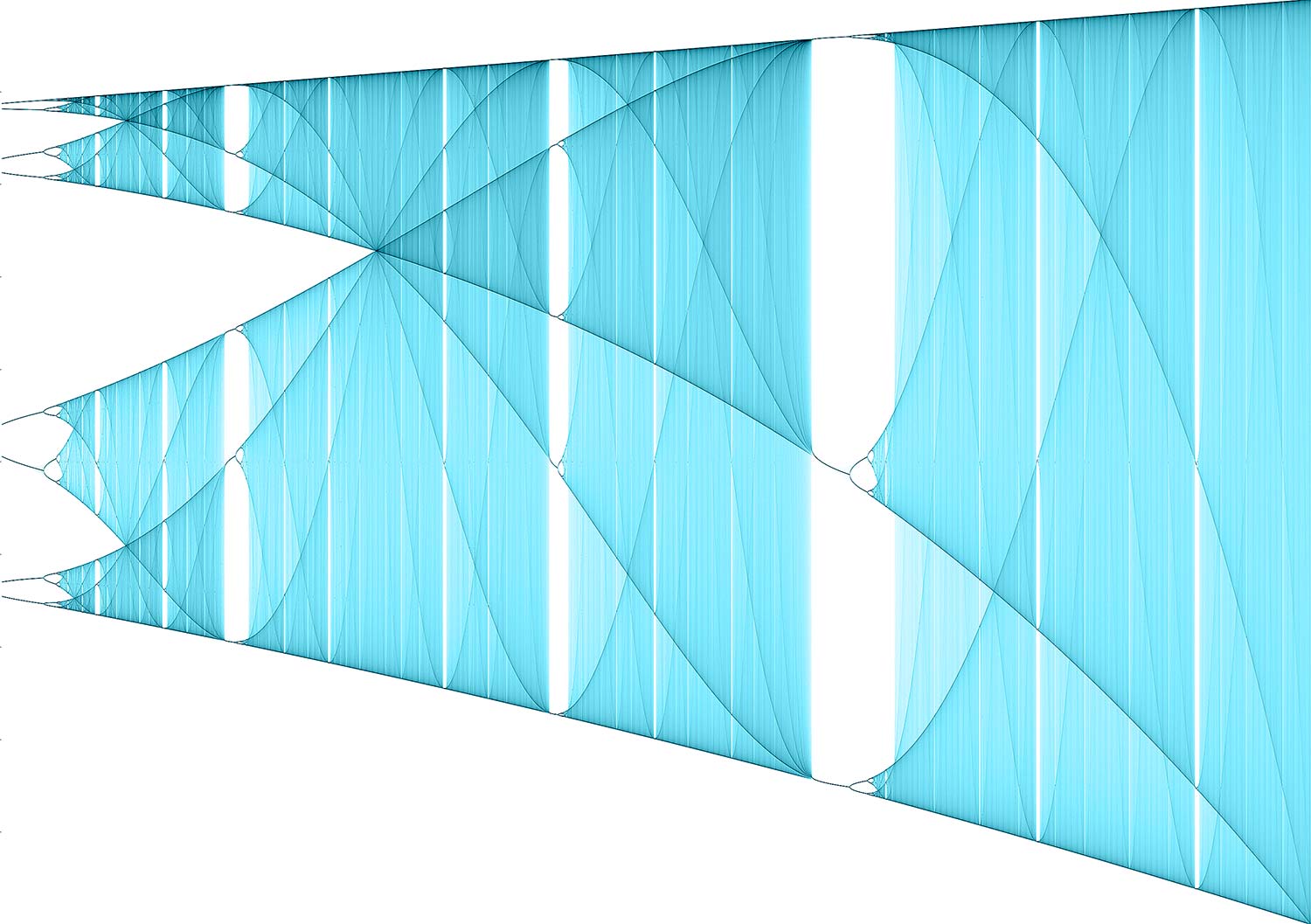
Ensuite, j’ai réussi à comprendre à peu près le bazar et j’ai pu faire des rendus de meilleure qualité comme plus haut et ci-dessous en 3000 x 4500 pixels, rendus en 222 secondes, soit 3,70 minutes, soit 0,06 heures comme me l’indique fort à propos ce logiciel qui sait compter…

La révélation

A force de regarder ces diagrammes de bifurcation dans le blanc des yeux j’ai commencé, premièrement à loucher, et deuxièmement à chopper un genre de vertige que j’aime particulièrement : celui annonciateur de la découverte de nouveaux concepts. Feingenbaum, c’est Mandelbrot ! Et inversement !

Comparons donc comme ci-contre les deux représentations : une courbe, qui se divise en deux, puis en quatre, puis en huit et bientôt en chaos, cela ne vous rappelle rien ? Essayez de « voir » l’ensemble de Mandelbrot, non plus en 2D mais en 3D, avec un axe « Z » de hauteur qui serait représenté par le diagramme de Feigenbaum justement.

On découvre l’apparition de la complexité et du chaos dans la branche horizontale, à gauche de l’ensemble, comme on s’y attendait mais aussi dans chaque sous ensemble sur le pourtour du cardioîde principal, ce qui correspond bien à l’apparition de motifs fractals complexes dans ces zones, comme on le constate dans l’animation ci-dessous…

 

Pour apprécier toute la beauté de ce concept, je vous conseille de regarder cette vidéo où l’on comprend vraiment bien deux notions essentielles.

Premièrement,  l’auto-similarité : quand on zoome dans le diagramme, on retrouve cette même forme « arborée » à toutes les échelles, ce qui est la caractéristique des fractales.

Deuxièmement l’alternance des zones grisées chaotiques ménageant entre elles une infinité de zones de stabilité (en clair) qui correspondent exactement à la position des « minibrots« , les unes permettant de localiser les autres ou inversement…

 

Et pour finir, si j’ai réussi à vous mettre l’eau à la bouche, regardez cette excellente production du canadien d’origine australienne Derek Muller (quel talent !) sur le site de vulgarisation scientifique Veritasium qui explique tout ! Il y est question de lapins et de robinets qui fuient. Bienvenue au choeur du chaos…