La notion de l’infini, ou plutôt des infinis passionne. Toujours. Un vertige accessible à tout un chacun et même aux plus jeunes qui comprennent facilement que dans la suite infinie des nombres par exemple, il est toujours possible d’ajouter « 1 » au plus grand d’entre eux, si grand soit-il… Oui, l’infini est à portée de notre main.
Quant au signe choisi pour le représenter, ce « huit » couché, rien de plus simple à tracer, même dans le sable du plus infini des déserts. Mais quelle est son origine ?
A l’origine de l’infini…
A première vue, on pense à un anneau de Moebius stylisé mais il n’en est rien. Georges Ifrah, dans son incontournable encyclopédie « L’histoire universelle des chiffres », explique que le graphisme de l’infini remonte à la civilisation indienne, et même à la mythologie indienne. L’Ananta (terme sanskrit qui signifie infini), le « serpent infini » du dieu Vishnu, est représenté enroulé sur lui-même à la manière d’un « huit renversé ».
Notons que l’on peut obtenir une bonne représentation de l’infini en traçant une Lemniscate de Bernoulli, courbe élégante et simple aux multiples propriétés dont celle de pouvoir être parcourue infiniment. C’est ainsi que l’on a pensé qu’elle était à l’origine du sigle infini mais, encore une fois, il n’en est rien.
Le signe « infini » a été inventé en fait par le mathématicien John Wallis, contemporain de Bernoulli et publié en 1655 dans De sectionibus conicis.
Un ouvrage que je vous recommande comme livre de chevet tant il est souverain contre la migraine (surtout en latin)…
Sa forme est effectivement similaire à la lemniscate de Bernoulli et à certaines configurations du ruban de Möbius.
Dans l’infini artistique…
Élégante la lemniscate ? Sans aucun doute. Et je la retrouve souvent dans mes explorations fractales comme ci-dessous dans le tableau Automne.
Collection Jungle – Automne
Bien entendu la lemniscate de Bernouilli est accessible dans la plupart des logiciels de 3D sous forme de courbe vectorielle qu’on appelle une « spline ». Dès lors, il est tentant de triturer l’infini à l’aide de diverses extrusions pour obtenir des solides 3D, infiniment étranges. Voici quelques-uns de ces infinis délires…
Merci infiniment ! 🙂
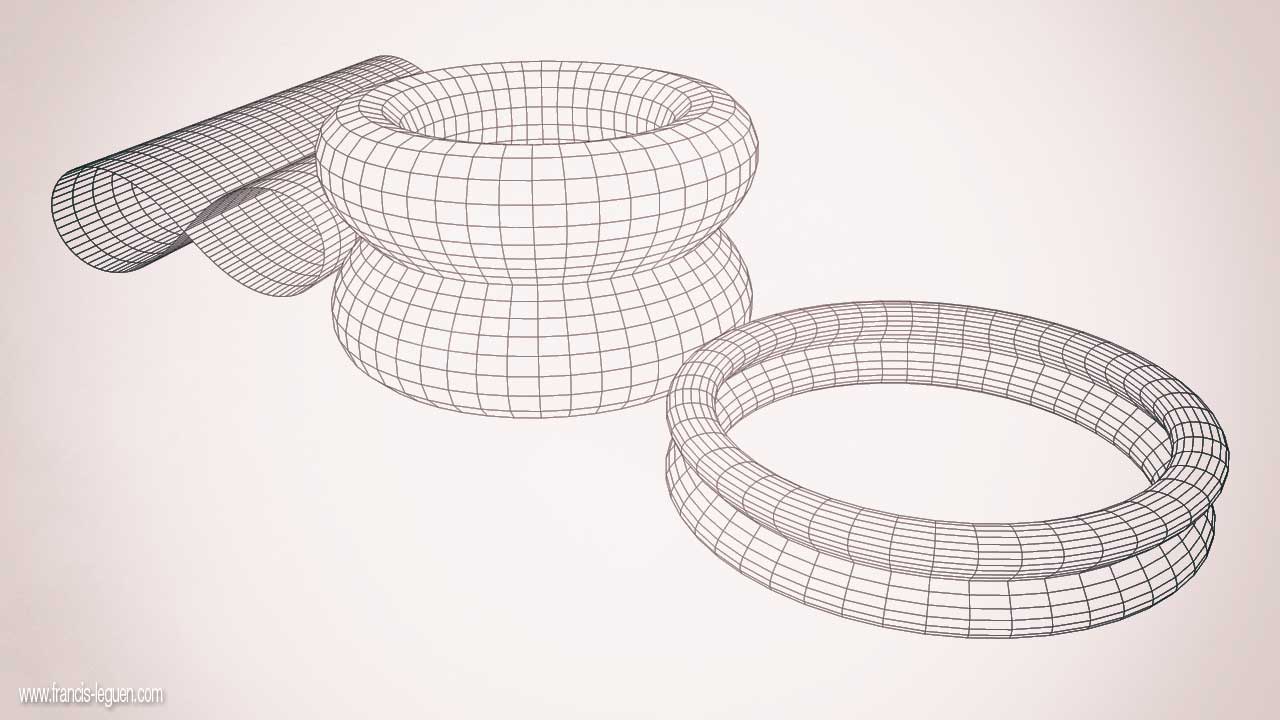
Sur la planche à dessin, de gauche à droite : Cylindre lemniscate et deux tores lemniscate…
Sorti des convulsions de TopMod…
Tore infiniment tordu… Réglisse et gelée d’hibiscus.
Cas particulier des anneaux borroméens. Attention, ça casse comme du verre !
Armoiries.
Le retour du tore.
Pièce unique. Porcelaine mauve. Infiniment chère…
Nouveaux fusibles. Pour péter les plombs infiniment.
Je suis de tout cœur avec vous.
Bonne fin de semaine !
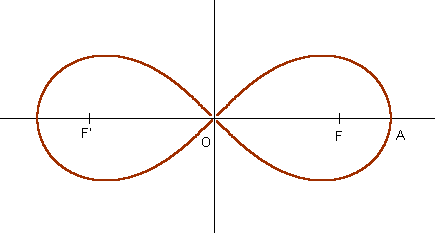
Très belles images, mais la définition pour moi c’est du brouillard
Vu mon seul titre « d’ancien élève des écoles communales de la ville de Paris » je n’ai retenu que le célèbre théorème qui dit « Tout corps plongé dans un liquide et n’ayant pas réapparu au bout d’une heure appartient au scaphandrier »