 Le problème avec nous autres humains c’est qu’on a tendance à raisonner, à penser, à appréhender ce qui nous entoure en 3 dimensions, celles qui nous sont familières : la largeur, la hauteur, et la profondeur… Une quatrième dimension est en principe facilement représentable, c’est le temps. Un objet est différent selon le « moment » où on le décrit : une glace qui fond par exemple.
Le problème avec nous autres humains c’est qu’on a tendance à raisonner, à penser, à appréhender ce qui nous entoure en 3 dimensions, celles qui nous sont familières : la largeur, la hauteur, et la profondeur… Une quatrième dimension est en principe facilement représentable, c’est le temps. Un objet est différent selon le « moment » où on le décrit : une glace qui fond par exemple.
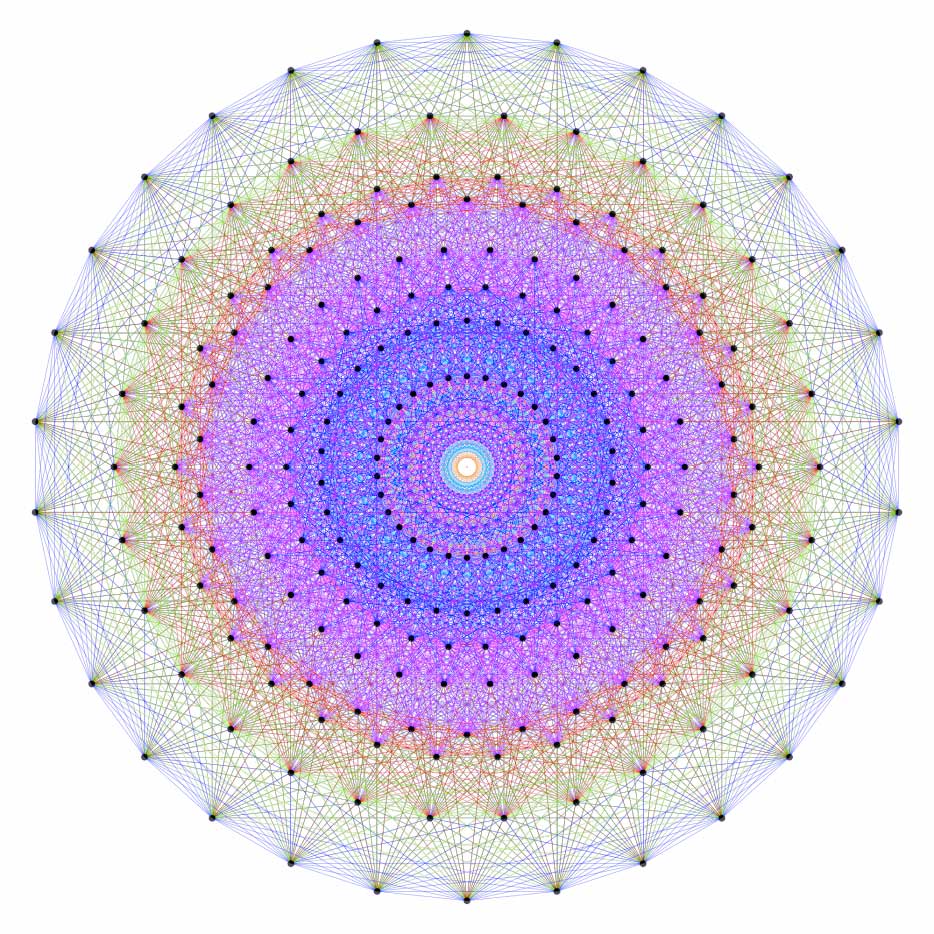
Mais la valse des dimensions qui régissent notre univers ne s’arrête pas là : les théoriciens décrivent et manipulent depuis longtemps 5, 6, 7 dimensions… Et l’on nous dit que la théorie des cordes (celle qui expliquerait tout et réunifierait les théories macroscopiques et microscopiques) exige 9 dimensions ! Si je ne dis pas de bêtises, le groupe de Lie E8 (autre percée dans la théorie du tout, représenté en 2D ci dessus) compte lui 248 dimensions… Cet ensemble qui évoque un mandala bouddhiste est par ailleurs considéré comme l’objet le plus complexe en mathématiques…
Mais comment se fait-il que toutes ces dimensions nous soient « invisibles » ? D’abord, rien ne dit que les humains soient équipés en standard de ce qu’il faut pour « ressentir » ces dimensions « cachées » de l’univers. Ensuite, ces dimensions seraient de taille minuscule et repliées sur elles même… Le tube d’aspirine est sur le buffet, derrière…
La 3D c’est dépassé : essayez au moins la 4D…
 Prendre un simple cube et tenter de se le représenter en 4 dimensions… Voilà bien une entreprise de cerveaux dérangés dont je m’honore de faire partie… Il se trouve que l’excentrique Salvador Dalí avait relevé le défi en 1954 en exposant sa peinture Corpus Hypercubus, exposé aujourd’hui au Metropolitan Museum of Art à New York et représentant la crucifixion non pas sur une croix mais sur un hypercube. Ou plutôt le « patron déplié » d’un hypercube…
Prendre un simple cube et tenter de se le représenter en 4 dimensions… Voilà bien une entreprise de cerveaux dérangés dont je m’honore de faire partie… Il se trouve que l’excentrique Salvador Dalí avait relevé le défi en 1954 en exposant sa peinture Corpus Hypercubus, exposé aujourd’hui au Metropolitan Museum of Art à New York et représentant la crucifixion non pas sur une croix mais sur un hypercube. Ou plutôt le « patron déplié » d’un hypercube…
En géométrie, le tesseract, (octachore) est le plus simple des hypercubes : c’est l’équivalent quadridimensionnel du cube. Le tesseract est au cube ce que le cube est au carré…
Ci dessous, deux représentations de la bête.

 Essayez de suivre des points remarquables et de vous faire une idée du « volume » en 4 dimensions. Attention, ça pique un peu les yeux… Au début.
Essayez de suivre des points remarquables et de vous faire une idée du « volume » en 4 dimensions. Attention, ça pique un peu les yeux… Au début.
Une autre dimension ?
Et maintenant, voyageons du côté des hypercubes à n dimensions, vertige garanti ! Voici par exemple les représentions des hypercubes de dimensions 7 et 15…

 Car il existe, bien entendu, des logiciels pour jouer avec ces étranges solides : Hypersolids (Mac) et Hypercube (Win).
Car il existe, bien entendu, des logiciels pour jouer avec ces étranges solides : Hypersolids (Mac) et Hypercube (Win).
 Je vous signale aussi au passage un bouquin fort sympathique sur ces sujets, que j’ai englouti il y a quelques temps. On y trouve quantité d’objets et de bizarreries mathématiques.
Je vous signale aussi au passage un bouquin fort sympathique sur ces sujets, que j’ai englouti il y a quelques temps. On y trouve quantité d’objets et de bizarreries mathématiques.
Un véritable voyage d’exploration ! Ah si seulement on m’avait appris les maths comme ça… Misère !




Extraordinairement dérangeant le Tesseract !
Oui, quelque chose d’assez gastro enterisant… MDR
Du coup j’ai exploré Youtube, et j’ai trouvé la chaîne d’un certain Oskar van Deventer, créateur de puzzles / rubik’s Cube étranges.. passionnant : http://www.youtube.com/watch?v=7SbOYXQ2x6I
Des puzzles en fractales : il y a des vicieux… 😉
Si tu regardes ses autres vidéos, il y’a des puzzles rubiks cube encore plus vicieux !!