 Continuons notre voyage au pays des bizarreries mathématiques. Je suis tombé sur un logiciel assez marrant qui permet de visualiser des surfaces de Seifert (pour simplifier, des surfaces « impossibles » comme l’anneau de Moebius mais en beaucoup plus vicieux). Ces surfaces sont issues de la complexe théorie de nœuds, qui prend tout son sens quand on cherche à se représenter un univers doté de multiples dimensions.
Continuons notre voyage au pays des bizarreries mathématiques. Je suis tombé sur un logiciel assez marrant qui permet de visualiser des surfaces de Seifert (pour simplifier, des surfaces « impossibles » comme l’anneau de Moebius mais en beaucoup plus vicieux). Ces surfaces sont issues de la complexe théorie de nœuds, qui prend tout son sens quand on cherche à se représenter un univers doté de multiples dimensions.
Dans Seifert Viewer, on peut manipuler les modèles à l’écran et essayer tous types de nœuds. Avec parfois la génèse de surfaces aux propriétés… Vertigineuses.
De quoi jouer des heures pour se rendre finalement compte que le plus court chemin d’un point à un autre n’est pas la droite…
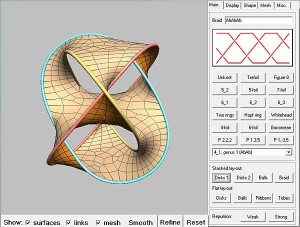 L’interface est simplissime. Pour chaque modèle il est possible de modifier la transparence, la lumière et les textures et de sauvegarder les images obtenues en jpeg. Une artiste a même utilisé ce logiciel pour produire d’étonnantes sculptures « en dur »… Il ne faut pas manquer, dans l’onglet display, de lancer l’animation « roller coaster ». [pullquote]Vous noterez au passage combien les scientifiques sont attachants : n’étudient-ils pas en physique la théorie des cordes et en topologie celle des nœuds ?[/pullquote]Il s’agit d’une caméra virtuelle embarquée sur un non moins virtuel wagonnet. Toujours est-il qu’on parcoure en temps réel des montagnes russes infinies. Sur une surface de Seifert, le voyage risque en effet d’être long…
L’interface est simplissime. Pour chaque modèle il est possible de modifier la transparence, la lumière et les textures et de sauvegarder les images obtenues en jpeg. Une artiste a même utilisé ce logiciel pour produire d’étonnantes sculptures « en dur »… Il ne faut pas manquer, dans l’onglet display, de lancer l’animation « roller coaster ». [pullquote]Vous noterez au passage combien les scientifiques sont attachants : n’étudient-ils pas en physique la théorie des cordes et en topologie celle des nœuds ?[/pullquote]Il s’agit d’une caméra virtuelle embarquée sur un non moins virtuel wagonnet. Toujours est-il qu’on parcoure en temps réel des montagnes russes infinies. Sur une surface de Seifert, le voyage risque en effet d’être long…
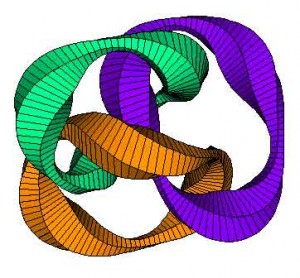 Il existe d’autres visualiseurs de ces surfaces et qui ne nécessitent pas de prise en main compliquée. Et même en ligne… Sur le site KnotZoo, qui utilise Java, il suffit de choisir un nœud de base, de modifier ses paramètres et le modèle est généré à l’écran. Le calcul est fait par le logiciel KnotPlot, qu’on peut aussi installer en local. Mais alors, bon courage : avec cette application, il n’y aura pas que des noeuds à l’écran..
Il existe d’autres visualiseurs de ces surfaces et qui ne nécessitent pas de prise en main compliquée. Et même en ligne… Sur le site KnotZoo, qui utilise Java, il suffit de choisir un nœud de base, de modifier ses paramètres et le modèle est généré à l’écran. Le calcul est fait par le logiciel KnotPlot, qu’on peut aussi installer en local. Mais alors, bon courage : avec cette application, il n’y aura pas que des noeuds à l’écran..
 Mais l’application la plus étonnante dans ce domaine est sans conteste Topmod, un logiciel gratuit et en français ; un modeleur de formes topologiques qui permet de créer des solides étranges, bien au delà de la géométrie d’Euclide… C’est un standalone c’est à dire qu’il ne s’installe pas, il est là, c’est tout. Comme quoi c’est possible… Double cliquez et à vous de jouer… L’interface est assez claire et moderne mais le produit qui est encore en développement souffre parfois de lenteurs assez exaspérantes. Pour vos essais n’allez pas tour de suite jouer avec les outils d’extrusion sur des solides à 3600 faces… Bref, le jeu consiste à créer un solide et à le creuser de diverses façons, à relier des faces par des ponts improbables avec un outil étonnant, à subdiviser, extruder jusqu’à obtenir très rapidement des modèles complexes qu’il serait bien difficile de modéliser avec d’autres outils. Il exporte dans différents formats pour pouvoir travailler l’objet dans d’autres logiciels. Pour commencer, un petit tutorial en français ! Ensuite, voici une liste detutoriaux vidéo plus ou moins difficiles.
Mais l’application la plus étonnante dans ce domaine est sans conteste Topmod, un logiciel gratuit et en français ; un modeleur de formes topologiques qui permet de créer des solides étranges, bien au delà de la géométrie d’Euclide… C’est un standalone c’est à dire qu’il ne s’installe pas, il est là, c’est tout. Comme quoi c’est possible… Double cliquez et à vous de jouer… L’interface est assez claire et moderne mais le produit qui est encore en développement souffre parfois de lenteurs assez exaspérantes. Pour vos essais n’allez pas tour de suite jouer avec les outils d’extrusion sur des solides à 3600 faces… Bref, le jeu consiste à créer un solide et à le creuser de diverses façons, à relier des faces par des ponts improbables avec un outil étonnant, à subdiviser, extruder jusqu’à obtenir très rapidement des modèles complexes qu’il serait bien difficile de modéliser avec d’autres outils. Il exporte dans différents formats pour pouvoir travailler l’objet dans d’autres logiciels. Pour commencer, un petit tutorial en français ! Ensuite, voici une liste detutoriaux vidéo plus ou moins difficiles.
Ceux qui maîtrisent l’engin (comme toujours) font des merveilles. Quelques galeries TopMod :
Galeries de James J. Lemon
[pageview http://www.topmod3d.org/gallery/main.php?g2_itemId=1224&g2_imageViewsIndex=0 « TopMod » Les galeries du site]




euh c’est un blog sur la plongée????!!!!!
😉
a quand des nouvelles de la grande bleue?
Aaaah c’est un blog perso, et pas seulement sur la plongée 😉 La Grande Bleue va bien, je l’ai sous les yeux ! Pour avoir de ses nouvelles, il va falloir attendre début mai la sortie du n° 2 de Plongeur.com : on a mis plein d’eau dedans !
Effectivement, même Chuck Norris ne se hasarderait pas à défaire de tels noeuds.
mais c’est pas dit qu’il en ai envie…. 😯
Même Chuck peut tomber en panne d’envie…
Ah merci pour ce « mind teaser ». Moi ça me rappelle la bouteille de Klein et son interprétation. Imaginer ce que l’on ne peut pas vraiment voir 😮
Bouteille de Klein, très juste… et tant de surfaces étranges : ces solides avec des trous qu’on appelle « fougasses »… A propos, Apogon, c’est un nom de poisson. Fortuit ou faites vous partie des « homo palmus » ?
Si vous aimez mes « mind teaser », vous devriez apprécier le billet sur la fonction Zeta, qui paraîtra mardi…
Le tore à n trou : la topologie est riche d’enseignements.
Oui, c’est une référence à l’Apogon imberbis : je suis étudiant en biologie marine.
Effectivement l’article de mardi m’interessera très probablement, je ne manquerez pas de le lire…