C’est la vague déferlante dans le monde des fractales… Daniel White, amateur de belles images et sans doute expert en maths, explique sur son site Skytopia comment il a créé la première représentation d’un ensemble de Mandelbrot en 3D, qu’il a appelé Mandelbulb. Bien sûr il existe d’autres générateurs de fractales qui donnent l’illusion de la 3D comme Apophysis 3D Hack ou Xenodream sur lesquels nous reviendront. Mais c’est la première fois que les fractales elles mêmes accèdent à la troisième dimension. Et cette découverte secoue la communauté des matheux. Sans entrer dans les détails rapidement vertigineux, rappelons que l’ensemble découvert par Benoit Mandelbrot (Lillois exilé aux US) est issu de l’élévation au carré de chaque point (nombres complexes) et génère des images qui gardent le même niveau de complexité et de détails quelque soit l’échelle, à l’infini. Les formes obtenues ressemblent beaucoup à celles rencontrées dans la nature : normal, la nature est régie par des lois fractales. Tripatouiller ces équations revient donc un peu à chatouiller les côtes de Dieu… Utilisant ce nouveau modèle, je me suis amusé à créer une vague qui rappelle un peu celle d’Okusai.
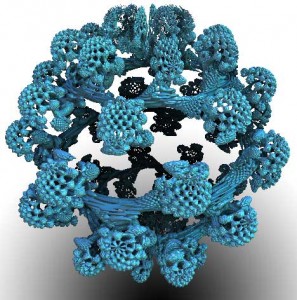
De son propre aveu, Daniel White n’est pas convaincu qu’il s’agisse d’un « vrai » volume de Mandelbrot, car il faut élever le point de base à la puissance 8 et non au carré pour obtenir des résultats intéressants. Mais c’est tout de même une avancée fantastique qui ouvre bien des pistes… Ci contre une représentation de l’ensemble de Mandelbrot en 3D que j’ai obtenue à partir des formules de White. Toute la question est de savoir comment utiliser ce nouvel algorithme et comment le visualiser ? Les logiciels générateurs de fractales habituels semblent inopérants. En fait il faut charger le fichier .pbk généreusement fourni par l’auteur dans un logiciel exotique : 3D mandelbulb raytracer en ayant préalablement installé le nom moins exotique Adobe pixel blender toolkit dont j’ignorais jusqu’à l’existence et qui est disponible dans les pages Labs d’Adobe qui regorgent de semblables richesses (On y trouve en ce moment une beta de Lightroom 3, si, si !). Dès lors, on a accès à un certain nombre de réglages et on peut triturer la Mandelbulb, la modifier et l’explorer à loisir.
Pour tout dire, cela me fait rêver. Car si pour l’instant toute la 3D produite se regarde en « 2D » sur écran ou sur papier, le temps n’est plus très loin ou nous allons pouvoir nous immerger directement dans un monde 3D… Explorer cette « sphère » de fond en comble (c’est à dire par définition à l’infini) en se promenant directement dedans doit être une expérience fascinante : de quoi occuper la vie d’un homme !
Autre perspective : la ressemblance avec la genèse de notre univers. On sait qu’au début il n’y avait rien qu’une « singularité », un néant pourvu d’information (mathématique ?) qui aurait donné naissance au big bang et à une expansion faisant apparaître tout ce qu’on connait y compris nous mêmes… Quand on cherche à remonter vers nos origines on se heurte au « mur de Planck« , une limite infranchissable au delà de laquelle les lois de la physique n’ont plus cours. Ceux qui ont entrepris ce périlleux voyage prétendent avoir trouvé un monde initial constitué d’un seul zéro. Une information capitale et fondatrice qui contiendrait toutes les autres à venir lors de l’expansion. Certains l’appellent Dieu… La Mandelbulb vue de très loin n’est qu’un point, mais en s’approchant, on s’aperçoit qu’elle contient un monde… Infini ! Embarquez pour le voyage dont on ne revient pas…
[media id=23 width=590 height=460]
Et si on poussait l’expérience plus loin pour faire entrer les fractales dans un monde à 4 dimensions ? La quatrième pouvant être considérée comme le temps et donc servir à « animer » la vision obtenue… Quel spectacle ferait-on naître sur l’écran ? Avis aux champions des nombres complexes !
Vous trouverez plus d’infos sur ces sujets passionnants sur le site Mathematical Imagery de Jos Leys avec un article en français. Et sur le site du mathématicien Paul Nylander.
Bonjour,
Je me permets de porter à votre attention un article que j’ai publié sur l’hypothèse d’un l’Univers fractal en dimensions D = 2,726 8…
Cette dimension fractale D , qui est la dimension de l’énergie du vide quantique, est l' »éponge de Menger-Sierpinski ».
Vous trouverez cet article dans la revue « efferveSciences N°77,
de Juillet-Août.
Votre avis m’intéresse.
Mario Cosentino ( Professeur de Mathématique et de Physique )
Quelques références:
-Voir mes 2 tomes: Le « New Big Bang » et « Origine et destin de notre Univers par une nouvelle cosmologie »
-le site de : http://lempel.pagesperso-orange.fr/soleil_kotov.htm
Le problème avec les blogs c’est que les gens les lisent. Et quand on aborde des sujets un peu pointus, les scientifiques débarquent 😆 ! C’est à la fois flatteur et intimidant : je ne prétend pas être un spécialiste… Vos liens sont très intéressant. Je consulterais aussi l’article d’Effervesciences.
En jouant un peu avec les itérations de l’éponge de Menger dans les logiciels de génération de fractales, on se rend bien compte, en poussant vers l’infini, que le cube est constitué de vide. Comme la matière à l’échelle subatomique d’ailleurs… Ne reste que l’information initiale. Cette dimension 2,726….. à l’infini. Faut-il croire alors à un univers infini ?
C’est clair que nous ne comprenons pas le cosmos, plus bourré de matière et d’énergie noire que de choses observables. J’ai toujours pensé (d’un point de vue poétique) que les fractales avaient à voir avec ce « grand mystère » qui, je le crois tout en souhaitant le contraire, nous restera inaccessible. Si je me réfère à l’histoire des sciences et à l’anthropomorphisme qui est la règle, les « dimensions » de l’univers n’ont cessé d’être revues à la hausse. Rien n’indique que nous soyons un « mètre étalon » en la matière et la complexité de l’univers peut dépasser largement nos dimensions spatiales, temporelles, et les capacités de compréhension de nos cerveaux et des calculateurs qu’ils ont engendré. Mais votre hypothèse de la dimension fractale de l’énergie du vide quantique est passionnante. Log 20/Log 3 étant très proche, si j’ai bien compris, de la température du Fond Diffus Cosmologique. Troublant hasard, en effet. Et ce vide qui est tout sauf vide… :lol:.
Quelles pourraient être les applications concretes de ce genre de découvertes? J’avoue mon ignorance.
Mario COsentino
Bonjour
Notre Univers serait-il infini?
Non pour au moins 2 raisons.
1-Selon la théorie de New Big-Bang le Big-Bang aurait donné naissance à 2 Univers à parité opposée très distants l’un de l’autre et tournant autour du barycentre commun.
2-Le plus rngpetit trou de l » « éponge de Menger serait de l’ordre de la longueur de Planck.
Donc il y aurait une limite au vide quantique et à l’Univers.
Mario Cosentino
Bonjour
Pour le moment ce genre de dimension fractale découverte aurait une application en cosmologie par exemple dans l’interprétation du décalage spectral vers le rouge.L' »éponge de Menger » jouerait le rôle de filtre,ou d’un réseau, aux rayonnements électromagnétiques.D’ailleurs dans les spectres il manque des rayonnement.
En plus les objets fractals sont étudier en Lab°oratoire. Pour plus de détails voir la revue « efferveSciences » Juillet-Août 2011,N°77,pp26 à 30.
Heureux de savoir que je contemple le Mur de Planck (au moins en pensée) quand je me perds dans les vides de Menger. 😆
Limite à l’univers, oui, mais que pensez vous de la théorie de la « mousse quantique » et de l’hypothèse des multivers ? Cet espace là ne serait-il pas infini ?
Les mathématiques fractales sont d’ores et déjà utilisées et nécessaires au sein de quantité de logiciels d’imagerie et de traitement de signal. Génération de paysages, réduction de bruit, agrandissement d’images, etc.
Au même titre que les découvertes de Bezier (ingénieur chez Renault qui inventa les fameuses courbes vectorielles déformables présentes dans tous les logiciels graphiques), celles de Mandelbrot (autre français) ont révolutionnées l’informatique. Cocorico !
Mario Cosentino
Réponse à Fran6
Bonjour
« LA MOUSSE QUANTIQUE » ET « L’HYPOTHÈSE DES »MULTIVERS »
Dans le cadre du « New Big-Bang Fractal » ayant la dimension fractale en « éponge de Menger-Sierpinski » « LA MOUSSE QUANTIQUE » serait la « MER DE DIRAC » ( un vide quantique rempli d’électron virtuels). Cette « MER DE DIRAC » ferait perdre de l’énergie aux photons et se traduirait également par un décalage des raies spectrales vers le rouge MAIS SANS EXPANSION POUR NOTRE UNIVERS !…
La croyance en une expansion accélérée de notre Univers serait
un leurre basé sur une fausse interprétation.
Les chercheurs ont énormément de potentiel mais il faut avouer que l’Univers en AURA TOUJOURS PLUS!
« Tous qui brille n’est pas de l’o »r ainsi ne prenons pas « des vessies pour des lanternes »…
Aujourd’hui il existe une liste d’observations, presque exhaustive, qui PLAIDE CONTRE LA CROYANCE QUE NOTRE UNIVERS EST ENCORE AUJOURD’HUI EN EXPANSION ACCÉLÉRÉE…
Notre Univers aurait été en expansion pendant une durée de presque 18 milliards d’années et selon mes équations il aurait ensuite STOPPE sa dilatation. Notre Univers serait dans cette phase STATIQUE depuis au moins quelques 100 milliards d’années…
Pourquoi aurait-il STOPPE son expansion?
Une hypothèse qui serait plus qu’une hypothèse s’est que la « MER DE DIRAC » serait devenue FRACTALE en « ÉPONGE DE MENGER » .
Pour » L’ HYPOTHÈSE DES MULTIVERS » les quelques 400 équations du modèle cosmologique du « New Big-Bang » ne parlent qu’un d’un Big-Bang qui aurait donné naissance qu’à SEULEMENT 2 UNIVERS A PARITÉ OPPOSÉE…donc que de 2 bulles : une de matière et la seconde d’antimatière…
Merci de m’avoir lu.
PS: pour plus d’informations allez s.v.p. dans Google et mettre:
blog de mario cosentino
ou Soleil et ondes de Kotov
Merci de toutes ces perspectives… Il ne faudrait surtout pas que les deux univers de la théorie se rencontrent de nouveau… Pour le coup, on assisterait à un sacré réchauffement climatique !
Mario Cosentino
Enseignant en Mathématiques & Physique
Formation Universitaire Astronomie et Astrophysique
L’EXPANSION DE L’UNIVERS: UNE GRANDE ERREUR DÉMONTRÉE PAR L’ABSURDE? ( PARTIE I )
1.PREMIÈRE PARTIE: LA CAUSE DE LA GRANDE ERREUR…
2.DEUXIÈME PARTIE : LES OBSERVATIONS OU LA DÉMONSTRATION DE LA GRANDE ERREUR PAR L’ABSURDE…
N.B. : JE RAPPELLE QUE, SELON MES TRAVAUX DE RECHERCHE, LE BIG-BANG N’EST PAS LA CAUSE DES NOMBREUSES ABSURDITÉS QUI SEMBLENT SE POINTER A L’HORIZON COSMOLOGIQUE MAIS LE FAIT D’ACCEPTER OU DE CROIRE QUE NOTRE UNIVERS EST ENCORE AUJOURD’HUI EN DILATATION!
TOUJOURS SELON MES TRAVAUX DE RECHERCHE , PROCHAINEMENT, LES OBSERVATIONS ( ET NON LES ASTROPHYSICIENS, LES INGÉNIEURS, ETC., QUI TRAVAILLENT, DE PRES OU DE LOIN, A ÉLABORER DES NOUVELLES THÉORIES ET DES TECHNOLOGIES DE PLUS EN PLUS ASTUCIEUSES ET PERFORMANTES! ) SERONT DE PLUS EN PLUS ABSURDES!
C’EST DONC L’ACCEPTATION OU LA CROYANCE EN UNE EXPANSION GÉNÉRALE ( accélérée ou non ) DU COSMOS QUI SERAIT LA CAUSE DE CETTE GRANDE ERREUR!
Encore selon mes travaux de recherche, pour que l’Univers puisse avoir des étoiles, des galaxies et des amas de galaxies aussi proches du Big-Bang il faudrait que celui-ci puisse avoir un âge bien supérieur que seulement quelques 14 milliards d’années.
A l’heure actuelle aucun modèle n’explique de façon définitive la présence des premières étoiles à seulement quelques 200 millions d’années après le Big-Bang!
Voici quelques raisons qui interdiraient cette présence d’étoiles, de galaxies et d’amas de galaxies, dans un laps de temps aussi court — ce qui nous fait courir le risque d’être confronté prochainement
à des observations où on verrait des objets qui, pour qu’ils puissent exister à une époque quasiment contemporaine au Big-Bang, seraient nés AVANT LE BIG-BANG …
CETTE SITUATION SEMBLE, DE PLUS EN PLUS, NOUS CONDUIRE ( ET JE PENSE QUE VOUS ÊTES D’ACCORD AVEC MOI) A ÊTRE BIENTÔT CONFRONTE A UNE GRANDE ERREUR QUI NE POURRAIT-ÊTRE QUALIFIÉE QUE «DE MONSTRUEUSE ABSURDITÉ!»…
Voyons cela de plus près:
1.A cette époque nous savons que l’Univers était chaud et sans poussière. Or il faut de la poussière pour évacuer la chaleur augmentant à cause de la contraction d’un nuage ou collapse.
2.Nous savons également que l’expansion de l’Univers dilate le gaz
3.Pour la formation d’une galaxies elliptique le « temps de chute libre est celui pris par une particule pour rejoindre le centre depuis le bord du système » [1]. Et ce temps ne concerne qu’uniquement la durée qui est du même ordre de grandeur que le temps dynamique qui est de l’ordre de 2 milliards d’années [1]. On pourrait appeler cette durée la phase du collapse. Ajoutons qu’à cette phase la galaxie est loin d’être achevée ou ayant acquis le stade de maturité…
Maintenant ajoutons les observations d’ amas de galaxies ( de plus en plus nombreux ) à moins de 1 milliard d’années après le Big-Bang les discussions vont aussi être très «chaudes»…
Alors comment le modèle dominant explique-t-il l’ observation des galaxies et des amas de galaxies à moins de 1 milliard d’année seulement après le Big-Bang?…
N.B. : Attention : faire appel à la matière noire c’est vouloir résoudre un modèle hypothétique par une autre hypothèse…
Pour résoudre ce problème des galaxies précoces l’hypothèse d’un Univers d’au moins 100 milliards d’années ne semble pas déraisonnable à l’heure actuelle car le modèle cosmologique dominant rencontre de plus en plus de problèmes devant les observations de plus en plus fines…et les graves problèmes ne font que commencer…
Il est à noter que les observations montrent qu’il existe des indices de plus en plus nombreux qui plaident contre la croyance, généralement admise, que notre Univers est encore aujourd’hui en expansion accélérée!
Aujourd’hui il n’existe aucun modèle cosmologique qui résous toutes les grandes énigmes de notre Univers. Il est temps, pour faire avancer nos connaissances de confronter le modèle dominant avec d’autres modèles alternatifs. Mais pour cela il faut beaucoup de courage et un esprit ouvert pour se préparer à observer des objets « collés » au Big-Bang » qui, maintenant, nous font courir le risque de se trouver a se dire que « NOUS SOMMES EN FACE D’UNE GRANDE ERREUR! »…
Dans ce cas sommes-nous prêt à changer de paradigme quitte à perdre la face???
Affaire à suivre…
Pour plus d’informations concernant mon modèle d’Univers qui se nomme le « New Big-Bang Fractal » voir les références [2] et [3].
Références
[1] Jérôme Perez: « Gravitation classique Problème à N corps, de 2 à l’infini… », 2e édition, Les presses de l’ENSTA, 2011, pp. 105 à 109.
[2] Allez dans Google et mettre : mario cosentino ou blog de mario cosentino
[3] Pour connaître l’équation qui relie la température de notre Univers à 2,726 K et la dimension fractale de l’ « éponge de Menger-Sierpinski » égale à 2,726 8 allez dans Google et mettre : Soleil et Kotov
NB: mes travaux de recherche font l’hypothèse que notre Univers aurait une géométrie à dimension fractale égale à 2, 726 8… ou à « éponge de Menger-Sierpinski »…
Mario Cosentino
AU SUJET DU LIVRE «Un autre cosmos?» [3]
Enfin ! après quelques 25 années de patience ce livre «Un autre cosmos?» conforte les hypothèses du modèle cosmologique du «New Big-Bang Fractal» («NBBF») et où on lit que «C’est toute l’image du cosmos issue du modèle standard qui s’en trouve ébranlée». ( page 99 ).
La synthèse des points forts de ce livre, rejoint de façon surprenante la synthèse que j’ai publié au cours de mes 25 années de recherche et contenue dans mon tome 2 (2001) [2] ainsi que dans mes Mémoires Académiques et articles dans les différentes revues publiées au cours de ces 25 années.
Donc ce livre vu qu’il conforte mes hypothèses de travail il me sert aujourd’hui de « tremplin » pour accréditer mon modèle d’Univers du « NBBF ».
Voici les points forts qui rejoignent, de façon très proche, étonnamment la synthèse du «NBBF»:
1- une répartition de la matière inhomogène (pages 35 et 107).
Selon les équations du modèle cosmologique du « NBBF » la gravitation, dans cet Univers inhomogène, ne joue qu’un rôle secondaire ( ou local ). Les équations du «NBBF» décrivent plutôt un Univers globalement quantique et fractal.
2- la répartition de la matière en «éponge» (page 36) .
Dans le cadre du « NBBF » la valeur de la dimension fractale D, valeur intrinsèque du vide quantique, serait celle qui correspond à l’ « éponge de Menger-Sierpinski » avec D = 2, 726 8 K. Cette dimension fractale est extrêmement proche de la température de notre Univers qui, comme nous le savons, est de 2,726 K! Selon le « NBBF » l’expansion de l’Univers aurait durée 18 milliards d’années. Cette phase de dilatation elle se serait faite par de nombreux « sauts quantifiés ». Après cette phase d’expansion quantifiée notre Univers serait devenu complètement statique. Pour qu’elle raison ? Car il serait devenu globalement fractal. Cette hypothèse est une extrapolation qui repose sur un certain nombre d’expériences menées sur des surfaces fractales à l’ École Polytechnique près de Paris. De ce fait cette hypothèse est plus qu’une hypothèse !
3- sur l’existence de 2 Univers ( page 91 ).
Dans le modèle du « NBBF » ces 2 Univers sont très éloignés l’un de l’autre car il s’agirait pour le premier de matière et le second d’antimatière. Le « NBBF » répond donc à la question : « où est donc passée l’antimatière ?»
4- ««l’existence de points chauds et froids opposés sur le ciel, définissant un axe privilégié, baptisé « l’axe du diable » par l’astrophysicien Joao Magueijo »» (page 93). Cet axe est prévu dans l’Univers sphérique du « NBBF » car dans ce modèle le cosmos tournerait, très lentement, autour de cet « axe ». D’ailleurs, en Novembre 1997, la revue Sciences et Avenir, Le Figaro, etc, m’ont appelé « le père de l’axe de l’Univers » ( Sciences et Avenir N°609, Novembre 1997).
5- la mise en doute de l’expansion de l’Univers (page 25, 39). (…) Dans ce cas, ce dernier ne serait pas en expansion mais statique. » (page 44, 92, 117, 118 et 143).
-C’est moi qui souligne.
Officiellement c’est depuis mars 1990 que je soutiens l’hypothèse que notre Univers ne serait plus en expansion (voir mon Mémoire déposé à l’ Institut de France Académie des Sciences de Paris, accepté en sa séance du 19 mars 1990 ainsi que mon tome 1 référence [1] ). Dans cette hypothèse depuis combien de temps notre Univers serait-il dans cette phase complètement statique? Selon le « NBBF » et l’observation des très grandes structures galactiques de l’Univers cette durée serait d’au moins 100 milliards d’années…
Petite chronologie d’un modèle d’ «Univers statique » ou «globalement statique»:
1642-1727 : Sir Isaac Newton
1915-1917 : proposition par Albert Einstein
1917 : de De Sitter
1978 : Georges Ellis ( page 40 )
1990 : Mario Cosentino ( Mémoire à l’Institut de France Académie des Sciences de Paris )
1992 : André Assis ( page 92 )
2006 : David Crawford ( page 92 )
2006 : Thomas Buchert ( page 118 )
NB : de tous ces modèles d’ Univers statiques quel est celui qui est le plus conforme aux observations les plus modernes?
Avec beaucoup de modestie et d’humilité il semble, à ma connaissance, que c’est le modèle cosmologique du « NBBF » car à lui seul il réuni, globalement, les points suivants qui constituent la synthèse du livre « Un autre cosmos ? » ainsi que la synthèse de l’ensemble des hypothèses du « NBBF ». Voici les point forts de cette synthèse :
1) Un Univers avec un Big-Bang donnant naissance à 2 Univers ( voir le point fort n°3 )
Il n’est pas exclu que notre Galaxie ou notre Univers communique avec ce second Univers ( voir les travaux de recherche de l’équipe du physicien Michael Sarrazin, Université de Namur, où ces chercheurs « estiment que le processus s’est déjà produit sans avoir été observé lors de certaines expériences ». Pour plus de renseignements à ce sujet lire l’article paru dans Automates Intelligents du 28 janvier 2012 de Jean-Paul Baquiast et Christophe Jacquemin sous le titre :
« Notre galaxie pourrait communiquer avec d’autres univers »
2) Un Univers avec expansion suivie d’une phase où l’Univers ne serait plus en expansion « mais statique » ( voir le point fort n°5 )
3) Un Univers qui deviendrait statique dès qu’il serait devenu entièrement fractal . La propriété fractale STOPPERAIT son expansion (voir le point fort n°2 ). La valeur fractale proposée par le « NBBF » est de D = 2, 726 8 qui est le volume fractal de l’ « éponge de Menger-Sierpinski ». Sur cette propriété fractale de notre Univers que disent les observations ? :
– plus on regarde loin, dans l’Univers, plus la dimension fractale D = 2,726 8 est compatible avec les observations. Il est intéressant de constater qu’un Univers qui serait fractal aurait les propriétés suivantes:
-les structures fractales entraînent la « stabilité ».
-les structures self-similaires peuvent s’interpréter comme des lois universelles.
-un Univers qui aurait une température constante favoriserait l’apparition de la dimension fractale.
Pour plus d’information concernant ces propriétés voir l’article de LA RECHERCHE N°313 – 10/ 1998 : « la gravitation façonne l’univers en fractals ».
Voir également : « Des fractales dans le vent solaire!» observées tous les 11 ans par Sandra Chapman et al. De l’Université de Warwick ( pour avoir accès rapidement à cette référence allez dans Futura Sciences et mettre: « Des fractales dans le vent solaire! ».
4) Un Univers statique qui devient inhomogène ( voir le point fort n°1 et 2 )
5) Une température de l’Univers à 2,726 K qui serait une propriété intrinsèque du vide quantique (voir le point fort n°7 )
6) Un Univers qui aurait un « axe privilégié » ( voir le point fort n°4 )
6- « D’autres chercheurs, comme le physicien André Assis, ont proposé que le fond diffus correspondrait à l’émission de la matière à une température de 2,7 K, dans le cadre d’une cosmologie sans expansion, où le décalage vers le rouge est interprété comme une «fatigue de la lumière», c’est-à-dire une perte d’énergie de la lumière sur son trajet 2 . » (page 92). 2 : André Assis, On Hubble’s law of Redshift, Olbers’ Paradox and the Cosmis Background radiation » Apeiron, 12, 10-16, 1992.
– C’est moi qui souligne l’expression « sans expansion ».
7- la température de l’Univers à 2,7 K comme «rayonnement universel emplissant la totalité de l’espace et produit aussi bien localement qu’à de grandes distances ? » (…) . La similitude de toutes ces températures entres elles et avec celle du fond diffus n’est peut-être pas une simple coïncidence. (…). Autrement dit, il semble plutôt facile de produire partout dans l’univers une température « universelle » de quelques degrés au-dessus du zéro absolu. C’est ce raisonnement qui guida plusieurs scientifiques pour proposer une explication alternative au 3 K . » ( pages 86 et 87 ).
Selon le « NBBF » cette température serait une propriété intrinsèque du vide quantique.
Par rapport à cette explication le « NBBF » soutien l’hypothèse que la température d’équilibre à 2,726 K est une propriété du vide quantique de l’Univers et serait une constante donc indépendante du temps qui passe.
Dans ce cas là notre Univers n’aurait pas à subir une « mort thermique » par une rapide congélation car il s’autorégulerait et se régénérerait pour l’éternité !
8- le décalage z vers le rouge « à cause d’une interaction gravitationnelle ».
Cette interprétation est donc « une interprétation non cinématique » (page 39) . Cette interprétation est celle de la théorie de «la fatigue de la lumière » d’Einstein, de l’astrophysicien Fritz Zwicky (le «père» de la matière noire») , et bien d’autres ainsi que celle du « NBBF ».
9- «l’ accélération (…) , pourrait être une illusion» (page 43), 37 et 118.
Dans le modèle du « NBBF » il n’y a plus d’expansion de l’Univers.
10- en 1964 Sir Fred Hoyle obtient un résultat très étonnant : « la quantité d’énergie produite par la fusion de l’hydrogène pour produire tout l’hélium observé dans l’univers est exactement celle contenu dans le fond diffus. En calculant la température de l’espace correspondant à cette énergie ils trouvent ainsi une valeur de 2,78 K ». ( page 88 ).
N.B. : le modèle du « NBBF » pour la température de l’hélium superfluide est de 2,18 K . Cet Hélium superfluide serait le constituant de la matière noire. Cette rayonnement lui aussi pourrait être « dégradé » . (page 88).
11- dans cet ouvrage, à de nombreuses reprises, il est utilisé le mot « paradigme ». (pages 115, 134 et 138 ).
Personnellement cela fait maintenant quelques 25 que je l’utilise lorsque qu’il m’arrive encore de tirer la « sonnette d’alarme »!
CONCLUSION
Depuis la sortie de ce livre je peut dire, avec modestie et humilité, que le modèle cosmologique du «NBBF» semble être entré dans son « âge d’or » !
Par contre devant les observations les plus actuels le modèle d’Univers dominant devient de plus en plus douteux [ 4 ].
Les problèmes que ce modèle rencontre sont trop nombreux pour être cités dans ce courrier. La très longue liste de ces problèmes a été recensée dans mon tome 2 [ 2 ].
Tout cela est très bien résumé par la revue scientifique LA RECHERCHE où nous lisons tout simplement :
« Modèle à revoir » [ 5 ].
Les informations contenues dans ce livre sont très pertinentes. J’encourage vivement toutes les personnes qui s’intéresse de près ou de loin à cette question, et qui veut se mettre à jour, à prendre connaissance de cet ouvrage car il est détaillé et très accessible.
Au regard de ces deux synthèses, très proches l’une de l’autre, ainsi que de mes différentes publications, nous constatons que le modèle du « NBBF » est un modèle cosmologique explicatif alternatif plus que satisfaisant . Les observations ne contredisent pas les nombreuses hypothèses du «NBBF». Donc au regard des observations ce modèle semble être une bonne piste de recherche car il permet de prévoir un ensemble de phénomènes dont certains ont été confirmés tandis que d’autres sont en attente d’infirmation ou de confirmation ( parmi ceux qui sont en attente de confirmation certains sont sur la bonne voie) . En tout cas le modèle d’Univers du «NBBF» semble améliorer ce qu’on observe; ce modèle est justifié par sa cohérence interne et, comme on l’a déjà vu, par un certains nombre de ses prévisions qui ont été confirmées soit par les observations soit par les expériences. S’obstiner à ne pas en tenir compte on risque de passer à coté de quelque chose qui pourrait être fondamentale pour une meilleure compréhension de notre Univers. Je reste persuadé que l’approche, asymptotique, de la vérité ne sera jamais dans un unique modèle d’Univers mais dans la «synthèse des modèles cosmologique actuels » [2]. La fédération de tous les modèles plausibles pourra nous conduire vers « Un autre cosmos » !
Alors, en guise de conclusion, voulons nous vraiment «Un autre univers ? »
Dans ce cas sommes-nous prêt à changer de « paradigme »?…
-Pour plus d’informations concernant mes travaux de recherche allez dans
Google et mettre: mario cosentino
Google et mettre: blog de mario cosentino
http://fdier.free.fr
http://lempel.net et aller dans Google et mettre: Soleil et onde de Kotov
-dans «Soleil et ondes de Kotov» se trouve l’équation qui relie la température de notre Univers et la dimension fractale de l’«éponge de Menger-Sierpinski».
Google et mettre: automates intelligents 84
Google et mettre: automates intelligents 113
Google et mettre: automates intelligents 116
REFERENCES
[1] Mario Cosentino: «Origine et destin de notre Univers par une nouvelle Cosmologie De l’atome jusqu’aux confins du Cosmos» Conversation avec Pierre Bourge. Bonnefoy – Imprimeur-Editeur, 1993
Références INIST ( Institut de l’ Information Scientifique et Technique ): 1/1 – ( C ) CNRS Numéro
PASCAL 93-0610460
Localisation: INIST-L 22828 . 354000035419100000
[2] Mario Cosentino: «Le New Big – Bang synthèse des modèles cosmologiques actuels» , Prologue de Bernard Milet, Astronome à l’Oservatoire de Nice, éditions Apolline, Chiron, 2001, ISBN: 2-84556-023-0
[3] « Un autre cosmos? » Sous la direction de Thomas Lepeltier et Jean-Marc Bonnet-Bidaud, Vuibert – mars 2012, auteurs : -Jean -Marc Bonnet-Bideau ( astrophysicien)
-Robert Brandenberger ( professeur de physique )
-Thomas Buchert ( professeur de cosmologie)
-Ludwik Celnikier ( directeur de recherche au CNRS)
-Stéphane Fay (Doctorat en cosmologie)
-Thomas Lepeltier (Historien et philosophe des sciences. Chargé de cours à l’université d’Oxford. Une de ses recherches est tournée vers la cosmologie moderne.)
-Jayant V. Narlikar (est professeur émérite de cosmologie à l’Inter- University Center for Astronomy and Astrophysics ( Pune, Inde) )
[4] An Open Letter to the Scientific Community, cosmologystatement.org
(Published in New Scientist, May 22, 2004
[5] LA RECHERCHE , SEPTEMBRE 2004, N° 378, page 10
Merci de ces précisions détaillées, riches de perspectives…
Ce serait intéressant de voir à quoi ressemblent les fractales « correspondantes » à la température de l’Hélium superfluide (dimension 2,18 ?) : une visualisation « artistique » de la matière noire ?…
Votre phrase : « Dans ce cas là notre Univers n’aurait pas à subir une « mort thermique » par une rapide congélation car il s’autorégulerait et se régénérerait pour l’éternité ! » me fait penser aux boucles de rétroaction positive qui semblent régir le climat de notre Terre et la vie qu’elle abrite (Hypothèse Gaïa et simulations « Daisy world)…
Mario Cosentino
à Fran6 ainsi qu’à tous les lectrices et lecteurs
Merci de me donner votre avis que j’apprécie. La valeur de 2,18 K et 2,726 K ont des dimensions de température à ne pas confondre avec la dimension fractale de 2,726 ( « éponge de Menger » ) qui est sans dimension.
Pour le reste de votre commentaire ( sur la non « mort thermique de notre Univers) c’est une intéressante idée à développer.
Cordialement
Mario Cosentino
Enseignant en Mathématiques & Physique
Formation Universitaire en Astronomie & Astrophysique
En 2003 félicitations d’un jury scientifique composé
d’un Astronome, d’un Physicien et d’un Géologue ( Université Jean Monnet de Saint-Etienne)
Chères lectrices, Chers lecteurs
Bonjour
LA COSMOLOGIE DOMINANTE EST DE PLUS EN PLUS OBSCURE!
Introduction
L’objectif de cet article est de nous faire prendre conscience que la situation actuelle de la cosmologie dominante est de plus en plus obscure, douteuse et qu’on a besoin d’un nouveau paradigme.
En effet, nous constatons que plus on explore, avec finesse , l’Univers proche et lointain plus ce dernier se montre de plus en plus mystérieux!
Cette situation paradoxale fait partie d’une des grandes prévisions ( qui remonte maintenant à 25 ans) de mes travaux de recherche rassemblés dans un modèle d’Univers qui porte le nom de «New Big-Bang Fractal» («NBBF») [ 1 ]. Les équation du « NBBF » disent que le Big-Bang aurait donné
naissance à 2 Univers à parité opposée ( voir mon blog à Google : mario cosentino ).
Les nombreux nouveaux défis les plus tenaces nous plongent dans un Univers de plus en plus mystérieux. Devant cet état de fait de plus en plus de spécialistes reconnaissent, enfin, que nous sommes à l’aube d’une révolution cosmologique (!).
Selon le modèle cosmologique du «NBBF» l’unique cause qui engendre tous ces nouveaux problèmes , n’est pas le Big-Bang mais de croire à l’hypothèse que notre Univers serait encore en expansion…
J’ai le plaisir et l’honneur d’exposer ici les résultats de mon étude.
1re partie: la situation actuelle de la cosmologie dominante ?CDM ou I?CDM pour I (Inflation, ? (énergie du vide) et CDM ( pour cold dark matter : matière noire froide).
Devant les observations les plus modernes la situation actuelle est vraiment plus qu’«obscure»:
Voici les grandes énigmes, non encore résolus , que l’on pourrait soumettre aux tenants de la cosmologie dominante:
1. On entend parler que notre Univers contient 95% d’inconnu: nous ne savons toujours rien sur la nature de quelques 25% de ce que nous appelons la matière noire (ou «obscure») , de quelques 70% d’énergie noire (encore de l’«obscure»). Enfin le seul pourcentage que nous savons ne concerne que les quelques 5% restant que constitue la matière qui est généralement lumineuse! Devant 95% d’ignorance comment est-il possible de bâtir un modèle d’Univers sur seulement 5% de connu?…Le modèle cosmologique dominant vous semble-t-il crédible surtout lorsque qu’il nous parle du devenir de notre Univers?
2. L’observation de galaxies presque contemporaines du Big-Bang dont certaines semblent très
vieilles car elles sont poussiéreuses
3. L’observation d’amas de galaxies également de plus en plus proche du Big-Bang
4. L’observation de filaments de galaxies allant jusqu’à constituer de gigantesques «murailles de galaxies».
5. Comment expliquer dans un Univers qui serait en expansion que l’Univers lointain ressemble globalement à l’Univers proche?
6. L’ homogénéité de la distribution de la matière lumineuse n’est pas encore démontrée.
7. L’observation du quasar OJ 287 [ 2 ] qui semble se situer dans notre Galaxies et non à une distance cosmologique. En effet ce dernier serait en phase avec l’activité Solaire ainsi qu’avec la période de révolution de Jupiter qui est la plus massive des planètes du système solaire. Si ce quasar ferait effectivement partie de notre Galaxie cela donnerait un coup fatal à tous les décalages spectraux vers le rouge interprétés comme un éloignement des galaxies.
Cela signifierait tout simplement que notre Univers ne serait pas en expansion mais globalement statique. Dans le cadre du «NBBF» cette phase statique aurait fait suite après quelques seulement 18 milliards d’années d’expansion…
8. Le problème de l’antimatière.
9. Même si elle a été l’objet d’un Prix Nobel l’expansion accélérée de l’Univers n’est pas définitivement prouvée
2e partie: analyses et critiques des spécialistes
Ici nous saluons le courage de certains spécialistes qui tiennent à bien nous informer sur la véritable situation de la cosmologie dominante.
Voici par ordre chronologique:
Francis Bernardeau chercheur au service de physique théorique du Commissariat à l’énergie atomique. Il a enseigné la cosmologie aux écoles doctorales d’astronomie et d’astrophysique et de physique d’île-de-France. Il a été directeur puis président du Programme national de cosmologie.
Voici ce qu’il dit au sujet de la matière noire et de l’énergie noire [3]:
«La nature de la matière noire, et de fait le détail de ses propriétés, nous est inconnue.» (page 350).
«Les observations montreraient que le niveau d’énergie du vide n’est pas triviale. C’est une situation quelque peu inconfortable ! On le voit le problème de l’énergie du vide est un réel enjeu de physique fondamentale. Sa résolution lèverait un peu le voile quant à la nature quantique ou géométrique de l’Univers.» ( page 351).
James A. Rich diplômé de Stanford et de Harvard, il est physicien au Commissariat à l’énergie atomique (Saclay).
Au sujet de l’accélération de l’expansion de l’Univers nous lisons:
«L’expansion s’accélère à l’heure actuelle. Si ce fait n’est pas considéré comme totalement établi, c’est uniquement parce qu’il est extrêmement surprenant.» (page 2).
Concernant la matière noire voici son commentaire:
«Par contre, la matière noire est par hypothèse formée d’objets réels massifs que l’on doit pouvoir rechercher et identifier. Avant qu’on ne l’ait fait, il subsistera des doutes sur le fait que la cosmologie
?CDM ait le moindre rapport avec la réalité.»[4]
-2-
Etienne Klein dirige le laboratoire de recherche sur les sciences de la matière au Commissariat à l’énergie atomique (CEA) et enseigne à l’École centrale.
Pour lui la situation est encore plus problématique car:
«L’univers pourrait donc être beaucoup plus vieux que l’âge qu’on lui attribue, voire ne pas avoir d’âge du tout. En ce sens, la question de savoir si l’univers est éternel ou non continue de se poser. Ne concluons donc pas de façon trop tranchée, d’autant que la cosmologie est peut-être au bord d’une révolution susceptible de complètement changer la donne. Deux problèmes sont apparus récemment- la «matière noire» et l’«énergie noire» – dont nul ne saurait prédire sur quels bouleversements conceptuels ils pourraient déboucher. Ils concernent l’un comme l’autre l’inventaire du contenu matériel et énergétique de l’univers: on vient de découvrir qu’une grande partie en était de nature parfaitement inconnue!» (page 106,107) [5]
Michel Cassé Astrophysicien de renommée mondiale.
Lui aussi à de nombreuses reprises il n’hésite pas à employé le mot REVOLUTION en rapport avec la cosmologie [6] ( Notez que la préface est de l’astrophysicien Hubert Reeves ) (!):
Nous lisons:
«La cosmologie est en révolution». (page 47).
«Nous sommes donc dans une position fort inconfortable, mais réjouissons-nous, cet inconfort fait peut-être signe vers une nouvelle révolution scientifique. Nous serions disent les indécrottables optimistes dans un stade prérévolutionnaire. Illusion peut-être, noble illusion. Il y a belle croyance dans la physique, croyance dans le progrès. La même différence d’interprétation se manifeste dans le registre de «l’énergie noire». Les géomètres, quant à eux, regardent le vide compulsif des quantiques avec répulsion. Bien que l’accélération tardive de l’expansion de l’univers semble empiriquement bien établi à partir d’analyses indépendantes des données cosmologiques, certains vont jusqu’à nier sa réalité, imputant l’effet à une non prise en compte du caractère inhomogène de l’univers et n’y voient qu’une pseudo-accélération due au caractère sommaire du modèle cosmologique ambiant insuffisamment ciselé. » (page 55).
«Il est néanmoins nécessaire de garder à l’esprit qu’une décennie après la découverte de l’accélération de l’expansion de l’univers, la cosmologie est plus un assemblage de modules théoriques, idées et inventions (…) mis bout à bout en réponse à l’observation, plutôt qu’un cadre théorique cohérent. Le modèle I?CDM n’est pas encore ancré dans des principes généraux et de ce fait il convient de vérifier ses idéalisations, rechercher ses déviations et trouver un fondement plus holistique. Chaque terme est en effet contestable, et a été d’ailleurs contesté. I, l’inflation, a résolu bon nombre de problèmes cosmologiques, et non des moindres, mais sa probabilité, pour certains, dont Roger Penrose, est négligeable. ? est obscur, et quand les physiciens des particules l’associent à l’énergie du vide quantique et le calculent, ils obtiennent un résultat extravagant. La matière noire, associée par les mêmes à un type de particules encore inconnu, suscite le scepticisme de plus d’un physicien.» (page 57 ).
«Pour conclure, l’expansion de l’univers semble s’accélérer au détriment de la connaissance cosmologique: les observations s’accumulent à grande vitesse, mais leur interprétation reste parfois obscure. On a l’impression de comprendre moins de choses aujourd’hui qu’il y a vingt ans.
L’astronome rompu à la dénonciation de l’illusion céleste, de la mythologie et de l’astrologie prône calme et discernement.
-3-
Mais les chevaux fous de la cosmologie quantique se sont pégasifiés semant la panique dans les observatoires ( mais n’en a-t-il pas été ainsi dans les laboratoires lors de la première révolution quantique touchant l’atome? ). Faut-il se désoler de cette débauche spéculative? C’est peut-être le signe d’une prochaine révolution scientifique.» ( page 91 ). —C’est moi qui souligne.
3e partie: propositions de solutions par le modèle cosmologique du «NBBF»
Le modèle cosmologique du «NBBF» semble résoudre de façon efficace les problèmes que nous venons d’évoquer. C’est un modèle logique ayant une cohérence interne. Dans toutes ses équations il n’existe aucun paramètre libre. Contrairement au modèle cosmologique dominant de nombreuses prévisions ont été confirmées et d’autres sont en bonne voie… D’ailleurs depuis mars 2012 la plupart des hypothèses de travail les plus importantes du modèle du «NBBF» ont les retrouvent étayées dans un ouvrage collectif [7] paru quelques 20 années après la sortie de mon premier livre! Cela est encouragent de voir que je ne suis plus seul à soutenir de tels hypothèses révolutionnaires!
La matière noire ( constituant 45 % de la masse totale de l’Univers) serait de l’hélium superfluide à une température de 2,18 K. Ses différentes propriétés physiques en font un excellent candidat à la matière noire. Une de ses propriétés serait de participer au maintien de l’équilibre de la température de notre Univers à 2,726 K. Si une certaine région du vide quantique inter-galactique aurait tendance à augmenter sa température l’hélium superfluide jouerait le rôle d’absorbant faisant ainsi baisser la température. D’ailleurs c’est pour cette propriété qu’il est abondamment utilisé dans les circuits du CERN.
L’énergie noire ( constituant 50 % de la masse totale de l’Univers ) serait un champ vectoriel qui contrebalancerait l’attraction de la masse baryonique constituée de 45 % de matière noire + 5 % de matière essentiellement lumineuse. Leur proportion de 50 % contre 50 % font que notre Univers pourrait se maintenir dans une phase globalement statique. Cette phase statique n’est pas possible dans un Univers gouverné uniquement par la gravitation dans le modèle de la Relativité Générale. Que notre Univers puisse être statique n’est pas à exclure car les oscillations relativistes du vide quantique pourraient participer à son équilibre global. Actuellement nous travaillons à un modèle théorique qui semble nous ouvrir de nouvelles pistes de recherche. Il concerne la modélisation d’un Univers par les équations de la mécanique des fluides ou les pressions et les contraintes déforment le «tissus» de l’espace-temps.[8] Cette modélisation fait appel à des disciplines scientifiques pluridisciplinaires ( la mécanique quantique, la thermodynamique, la mécanique des fluides, la Relativité Générale, la géométrie fractale, la physique des oscillations, la physique des plasmas, etc. ). Si vous désirez apporter votre contribution à ce travail de recherche très pointu, car novateur, nous vous souhaitons la bienvenue. Un ouvrage collectif est actuellement en préparation pour un très large public ainsi que pour les étudiants, les enseignants et les chercheurs. Merci de vous faire connaître en utilisant mon adresse électronique que voici:
mario.cosentino@hotmail.fr
Notre Univers serait devenu statique après quelques 18 milliards d’années d’expansion par sauts quantifiés. Pour quelle raison serait-il devenu statique? La réponse à cette question semble trouver une réponse dans l’hypothèse qu’il serait devenu globalement fractal… Cette explication est aujourd’hui plus qu’une hypothèse car des expériences, à l’École Polytechnique, semblent la soutenir par un certains nombre d’expériences [9].
Selon le «NBBF» la géométrie quantique de notre Univers aurait la dimension fractale de l’ «éponge de Menger» qui est de D = 2,726 8… valeur très proche de la borne supérieure de Tsirelson en physique quantique et valeur très proche de celle de e en mathématique.
-4-
Cette dernière valeur on la retrouve dans les calculs d’une expansion de l’Univers qui aurait été quantifiée et qui aurait durée 18 milliards d’années.
L’hypothèse, très plausible, de cette géométrie fractale semble trouver une explication qui reposerait sur des oscillations ou vibrations relativistes d’un espace-temps quantique. Autrement dit l’Univers vibrerait comme la « peau d’un tambour » et les galaxies seraient les «grains de sable » ou partie visible de cette « peau de tambour » en vibration.
Que notre Univers aurait été en expansion cela semble étayé par l’observation de distances privilégiées qui se seraient par la suite figées [10]. Ces distances privilégiées reposant sur l’observation de 264 000 galaxies présentent des pics à différentes échelles:
1. 0,41 million d’années-lumière pour la température de l’Univers [10]
2. 281 millions d’années-lumière pour des galaxies plus lointaines et [10]
3. 483 millions d’années-lumière pour des galaxies proches [11]
Ce qui est remarquable c’est que ces distances figées semblent faire ressortir, comme des empreintes , la structure de la géométrie fractale en «éponge de Menger» qui ne serait autre que le vide quantique.
Cette géométrie spatiale fractale, ou vide quantique, en «éponge de Menger» dans le cadre du «NBBF» nous donne pour ces distances privilégiées les valeurs théoriques suivantes:
1. 0,38 ( – 7% )
2. 266 ( – 5% )
3. 450 ( – 7% )
Les calculs sortent du cadre de cet article.
Depuis combien de temps notre Univers serait-il statique?
Les observations semblent indiquer que notre Univers serait âgé d’au moins quelques 100 milliards d’années ( 18 milliards d’années d’expansion + quelques 80 milliards d’années en phase statique ).
Cet âge, plus grand, rend possible l’existence des gigantesques structure galactiques ainsi que la présence des galaxies très bien structurées situées à des distances proche du Big-Bang.
Ainsi le simple rejet de l’expansion de l’Univers semble résoudre, à lui seul, la majorité des énigmes les plus tenaces. Vouloir continuer à croire à l’expansion de l’Univers semble nous conduire à des impasses de plus en plus graves et qui feraient non seulement perdre beaucoup de temps et d’argent mais en plus nous présenterait un Univers de plus en plus problématique car il s’éloignerait de plus en plus de la réalité…
Conclusion
Ainsi si nous faisons un bilan objectif de nos connaissances sur l’Univers que savons nous aujourd’hui?
Au regard de tout cela il est grand temps de reconsidérer la situation actuelle de la cosmologie dominante à la lumière des nouvelles observations commentées par des spécialistes qui deviennent de plus en plus nombreux et qui émettent des doutes sur la validité de ce modèle. Au lieu de penser que la vérité est dans un modèle et de ce fait on cherche à démolir le modèle de l’autre il serait plus profitable à la science de fédérer par une synthèse l’ensemble des modèles d’Univers existant sinon à vous de recouper toutes les informations afin de ne pas entendre qu’un son de cloche…
-5-
Alors la cosmologie dominante est-elle en crise?
Une conférence ayant pour titre:
«Crise dans la cosmologie» [12] s’est tenue fin juin 2005 à Monçao au Portugal. Voici un petit résumé, en 3 points, de New Scientist de cette conférence:
1.Le problème de la température de l’Univers
2.L’expansion de l’Univers
3.L’architecture et la répartition des galaxies.
Du fait que les prévisions ne sont pas conforment aux observations les cosmologistes du modèle dominant ajoutent des explications de plus en plus exotiques.
Laissons le mot de la fin à la revue Pour la Science:
«La cosmologie est-elle en crise? Question apparemment incongrue au regard de l’actuelle
prétention des cosmologistes d’avoir percé les secrets du cosmos. Cela dit, en science, on ne
reconnaît bien souvent une crise qu’après coup. Y aurait-il donc des signes d’une possible remise en cause de la conception dominante de l’Univers? Disons-le tout net: oui. » [13]
Références
[1] Voir les références de mes 2 livres et autres articles se trouvant dans la biographie de mon blog
[2] Voir le dossier contenu dans le site de Bernard Lempel
[3] Francis Bernardeau: «COSMOLOGIE DES FONDEMENTS THEORIQUES AUX
OBSERVATIONS», 2007, Savoirs Actuels EDP Sciences/CNRS Éditions
[4] James A. Rich: COSMOLOGIE, Vuibert, octobre 2010.
[5] Étienne Klein: DISCOURS SUR L’ORIGINE DE L’UNIVERS, Flammarion 2010
[6] Michel Cassé: «Astrophysique» Préface de Hubert Reeves, Éditions Jean Paul Bayol, 2011.
[7] «Un autre cosmos» , Sous la direction de Thomas Lepeltier et Jean-Marc Bonnet Bidaud, Vuibert, 2012
[8] Franck Delplace ( Diplôme d’Etudes Approfondies (DEA), Doctorat en mécanique, etc.) : «Porte ouverte sur la physique du 21ème Siècle », Imprimerie Jouve 1, rue du Docteur Sauvé 53 100 Mayenne
[9] Bernard Sapoval: «UNIVERSALITE ET FRACTALES», préface de Benoît Mandelbrot, Flammarion, 1997.
[10] LA RECHERCHE juillet-août 2011 – N°454, page 12. C. Blake et al. Monthly Notices of the Royal Astronomical Society ( l’époque dans LA RECHERCHE cela était à paraître ).
-6-
[11] BOSS / APC – AstroParticules . http://apc.univ-paris7.fr/APC_CS/content/boss
[12] Conférence Crisis in Cosmology http://www.allconferences.com/conferences/20050214090947/
Crisis in Cosmology. Discussion http://archive.ncsa.uiuc.edu/Cyberia/Cosmos/CosmolCrisis.html
Voir aussi «Automates Intelligents N°65»
[13] POUR LA SCIENCE -n°394- Août 2010, page 95.
Bonsoir
pour comprendre cette univers la raison ne suffit pas vous resterer bloquer sur la 3 eme dimention par besoin de materialiser pour la seule et bonne raison que ca rassure un monde qu on peut expliquer par a plus b des lors une infinite d hypothese aussi fumeuse les une que les autre emmerge de cette erreur de dissernement
a la raison vous devez ajouter la certitude qui est le fruit de la foi en un createur unique qui trancende tout
pour simplifier c est l onde originelle qui dicte les lois qui s applique lorsquil y a interaction entre l observeur et l ocean d infinie possibiliter
1 nous nageon dans un ocean infini de possibilite la parole du createur transcende cette ocean et lui donne cette structure merveilleuse selon sa volonter qui est notre univers regie par des loi en parfaite harmonie les une avec les autre
quand au humain le createur lui a donner son soufle ce qui lui permet d interpreter cette ocean de volonter infini par les cinq sens en devenant observateur notre ame applique un programmme gravitationelle inscrit dans ses genes a ce flux pour le decoder et lui donner une structure d illusion materielle crean ainssi un espace temp avec lequel il peux interagira a son tour
libre a lui d utiliser sa volonter comme bon lui semble
signe de l amour de son createur pour sa creature
en fait tout ce qui est visible est le fruit de l interaction de la volonter du createur et son ocean d infinie possibiliter plus le programme gravitationnelle de l observateur
je sais sais tout ceci est invisible donc non quantifiable
donc non prouvable bref a jeter
ben non je suis desoler vat faloir vous i faire ce que vous venez de lire est vieux comme le monde et demmeura ainssi pour l eternité
l univers aparait comme tres complexe mysterieux et mm efrayant pour ceux qui on peu de foi par contre tres reconfortant et rassuran pour ceux qui reconnaisse la signature de l infinie puissance de leur createur dans son oeuvre
les seule a avoir eu la connaissance de l interaction de l univers son les centaines de prophetes et messagers du Createur ils ont tous transmis ce savoir au hommes
mais peu on cru en eux nous somme a l heure de veriter
et leur triomphe eclate de partout il disais tous vrais…
tous ceux qui pretende pouvoir expliquer l univers par une equation qu il sache que les nombre n ont jamais rien creer c le contraire si rien n existait il n y aurais rien a compter…
Bonne soiree
Voilà une interprétation religieuse, en effet « vieille comme le monde ». C’est sûr que faire intervenir un « être transcendant » simplifie drastiquement le problème et les intentions de le résoudre si tant est que cela soit possible pour nous, pauvres humains…
Ce qui est fou avec les fractales c’est qu’elles suscitent des interrogations scientifiques, métaphysiques, religieuses… Que la lumière soit ! 😉